Note
This report was submitted to obtain a grade for COSC 3P99. It was originally made in Google Docs but I have converted it to markdown. The formatting will not look the same as it did in the document, so if there are any small formatting issues, please ignore them 🙂.
Info
Click here to access the TurboKnots Web Interface .
Abstract
The TurboKnots web interface [3] project involves developing an advanced web-based interface for Professor Thomas Wolf’s existing Linux-based knot theory software “TurboKnots”. This project aims to create a user-friendly platform that supports extensive functionalities such as real-time knot simplification, complex knot calculations, and broad import/export capabilities across various encoding types, such as MiniKnot, DT notation, and 4-tuple encoding. Unlike existing tools that are limited by their encoding formats or lack interactive features, TurboKnots provides detailed visual representations, dynamic adjustments, and comprehensive support for multiple encodings.
Introduction
This project originated with Professor Thomas Wolf from the Mathematics Department at Brock University, who has been developing “TurboKnots,” a Linux-based program designed to perform complex calculations on intricate knots, handling knot diagrams with up to 10,000 steps having up to 1000 crossings. Recently, after presenting TurboKnots at the “Knot Theory Informed by Random Models and Experimental Data” workshop hosted from the Banff International Research Station, Professor Wolf received significant interest from researchers who wished to use the program in their own work. However, TurboKnots, written in Pascal and currently compiled only for Linux, posed an accessibility challenge.
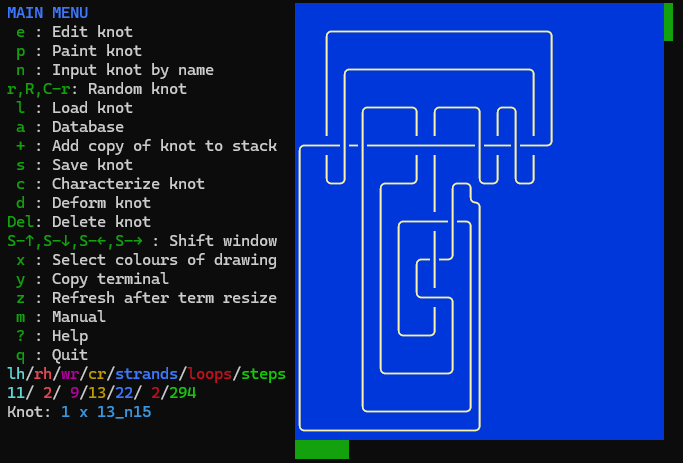 |  |
|---|---|
| TurboKnots Linux interface | TurboKnots web interface |
To address these challenges, the primary objective of this project was to develop an accessible, web-based interface for TurboKnots that would allow users to perform its functions on any device, operating system, or browser. This would make TurboKnots more widely usable, enabling researchers to research simplification of complex knots, to generate random knots, and to load knots based on their classification with ease.
A key requirement was the ability to support multiple knot encoding formats beyond the previously supported MiniKnot format, which encodes the layout on the grid and is therefore limited to the max size of the grid which is 255x255. By enabling users to import knots using more commonly accepted formats, such as DT notation and 4-tuple, the web interface would offer greater flexibility and cater to the diverse needs of researchers in the field.
Previous development work on a similar web interface was carried out by students Kindeep Singh Kargil and Liam Yethon in 2019, and Alex Van de Kleut in 2018. However, significant updates to TurboKnots and its modules have since rendered the earlier version non-functional. My task was to update and enhance the interface, ensuring compatibility with the latest version of TurboKnots while improving usability and accessibility.
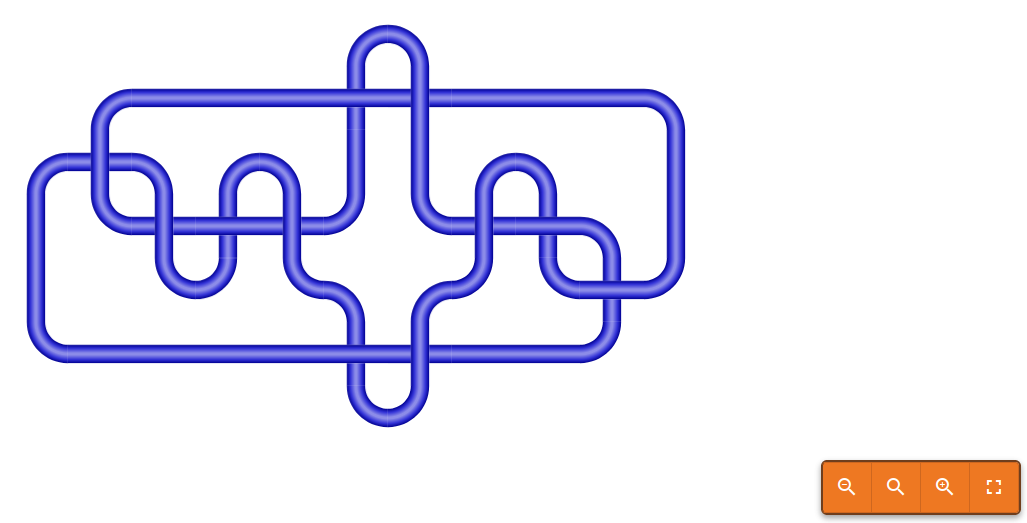 |  |
|---|---|
| Complex representation of the Unknot | The same knot simplified |
This project is significant not only for restoring and updating an existing tool but also for making TurboKnots more accessible to a broader audience. While the primary users are academic researchers, the web interface is designed to be intuitive enough for students and enthusiasts as well. Additionally, it has potential applications in educational settings, particularly in mathematics competitions and courses related to knot theory, aligning with Professor Wolf’s broader initiatives in mathematics education. [2]
Literature Survey
Theoretical Foundations
The Knot Book [1]
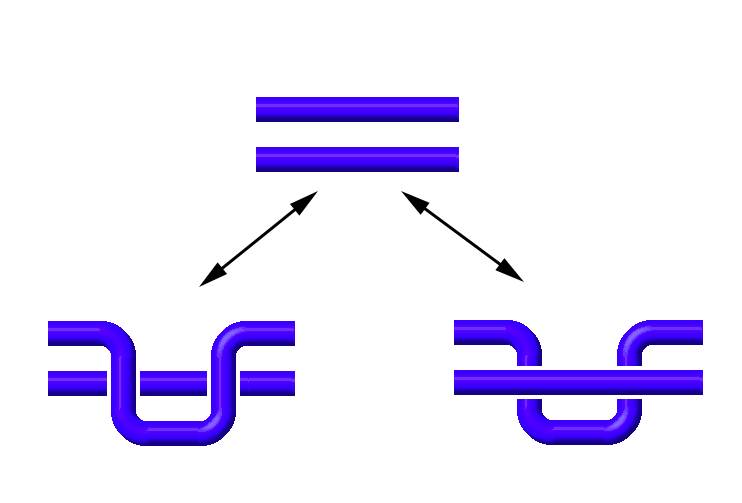
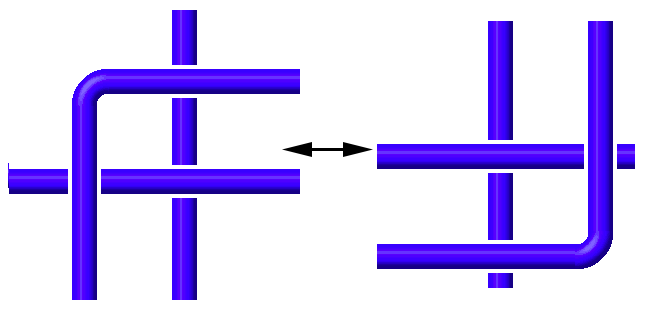
Using The Knot Book [1] by Colin C. Adams, I learned the foundational concepts in knot theory essential for developing a web interface for TurboKnots. The textbook provided insights into knot diagrams, which are crucial for visualising and manipulating knots. Reidemeister moves were also covered, which are fundamental for simplifying knot diagrams and determining knot equivalence. The textbook also introduced the concept of prime knots and knot invariants, which are essential for distinguishing and classifying knots.
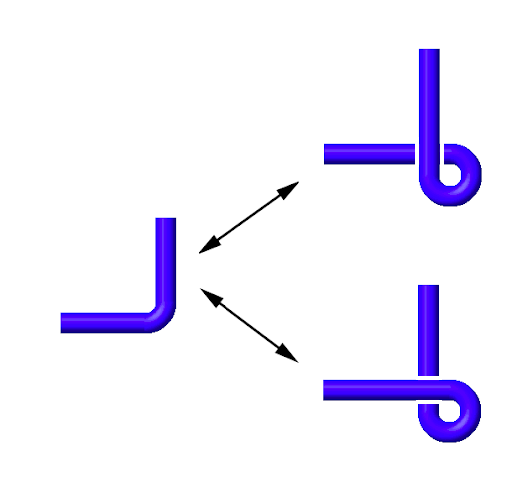 |  |  |
|---|---|---|
| Type I Reidemeister move | Type II Reidemeister move | Type III Reidemeister move |
Comparison of Existing Tools and Websites
Existing Tools and Websites
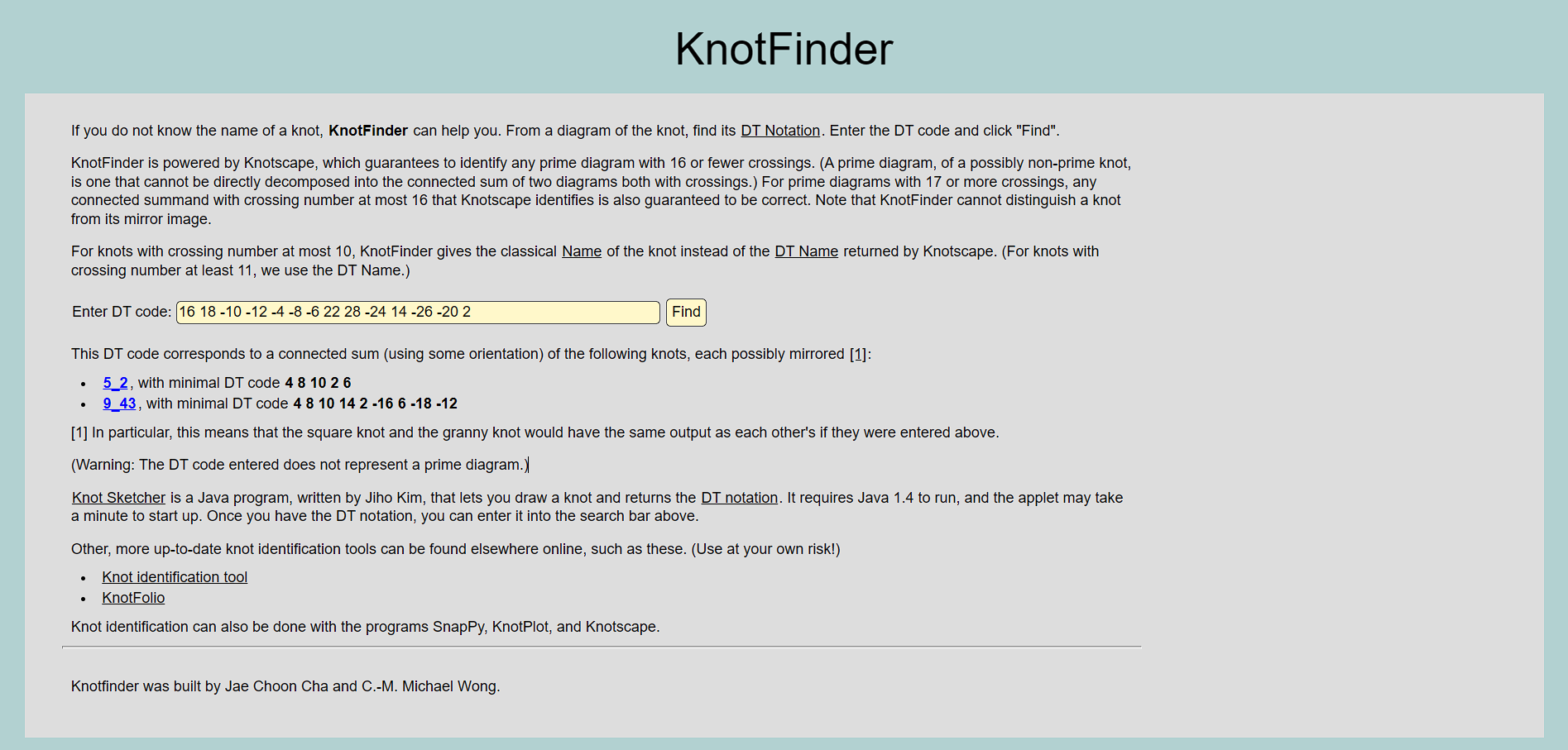
KnotFinder [4]
Created by Jae Choon Cha and C.-M. Michael Wong, KnotFinder is a tool that takes knots in DT notation and returns the knot name [7], as well as the minimal DT code. However, it does not provide visual representations of the knot, and is limited by only supporting DT notation.
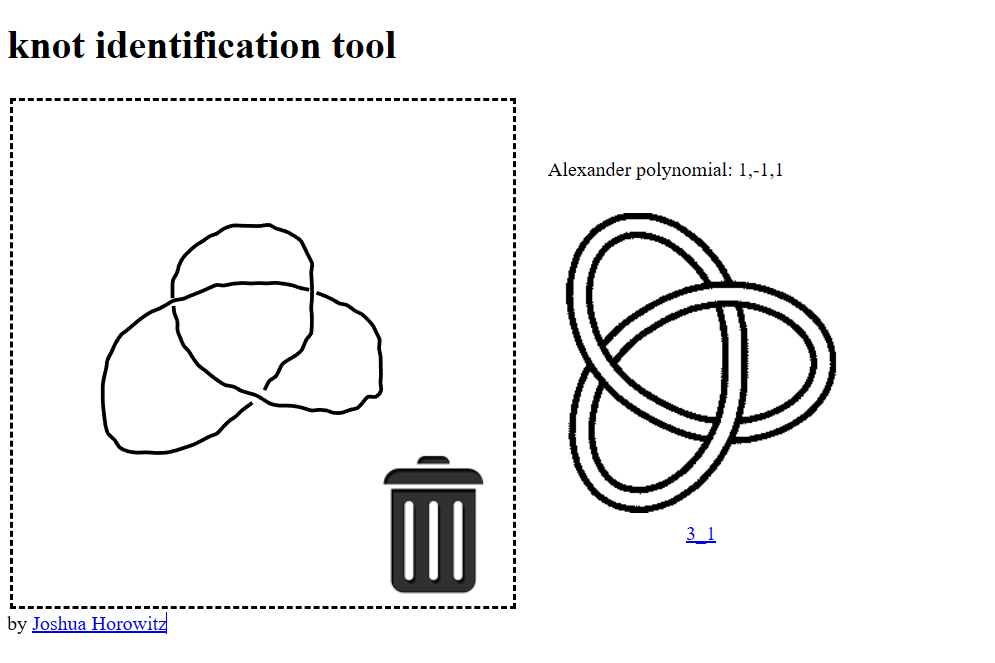
Knot Identification Tool [5]
Created by Joshua Horowitz, this tool allows users to draw a knot and provides the knot’s name (e.g. 3_1) and the Alexander polynomial. It offers a visual representation, which aids in understanding the knot’s structure, but it does not support a wide range of encodings or formats.
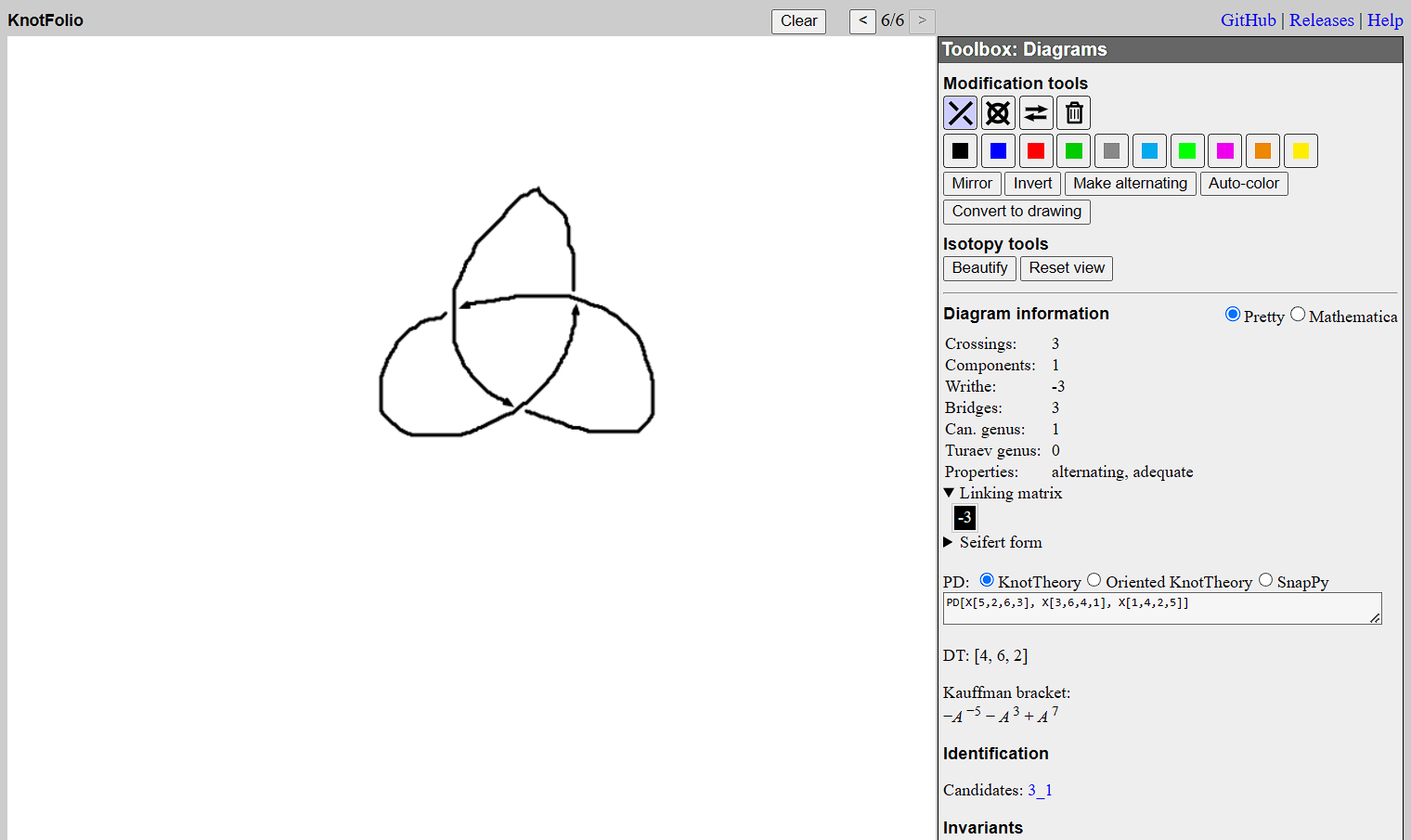
KnotFolio [6]
Created by Kyle Miller, KnotFolio offers similar functionalities to the Knot Identification Tool but with additional features. It allows users to draw a knot and returns the knots name, DT notation, Kauffman bracket, Alexander polynomial, (cabled) Jones polynomial, and Conway potential. This tool also includes the capability to classify knots that overlap in the same diagram, offering a more detailed analysis compared to other tools.
Comparisons to Existing Tools and Websites
TurboKnots separates itself from existing tools by offering a more comprehensive set of features and greater flexibility in handling knots. Unlike KnotFinder, which is limited to returning minimal DT codes without visual representation, TurboKnots provides detailed knot diagrams and relevant information. This visual and informational richness enhances user understanding and analysis of complex knots.
Advantages of TurboKnots
- Supports a broad range of import/export formats and encodings, including MiniKnot, 3-dimensional, 4-tuples, net, Gauss encoding, a custom format that stores sequences of diagrams for visualising deformations, DT notation, LaTeX, and HTML.
- Allows users to reduce knots to their simplest form and view changes dynamically.
- Includes real-time interactive capabilities, unlike the Knot Identification Tool and KnotFolio.
- Computes HOMFLYPT polynomials, a knot invariant that generalises both the Alexander and Jones polynomials.
Methodology
Background and Motivation
Motivated to make TurboKnots more accessible, Professor Wolf approached me to collaborate on a project to develop a web-based interface for TurboKnots. The goal was to create a platform that would be usable by anyone, regardless of their technical proficiency, and accessible on any device or operating system. The focus of this project was to maintain the robust functionality of TurboKnots while delivering it in a modern, intuitive, and platform-independent format. By developing this web interface, the project aims to bridge the gap between the technical nature of TurboKnots and the broader community of mathematics researchers, educators, and students who could benefit from its advanced knot manipulation capabilities.
During the workshop (https://www.birs.ca/events/2024/5-day-workshops/24w5217), which focused on random knots and the distribution of their sizes, Professor Wolf received specific feedback that further propelled development on TurboKnots. While TurboKnots was the only program capable of efficiently simplifying large knots, some examples presented at the conference were too large to be processed within the program’s current constraints. The limitations were particularly noticeable in knots given in a 4-tuple encoding, where crossings do not have a saved x and y component, making it impossible to compute their diagram on TurboKnots’ 255x255 grid. Recognizing this limitation, further development was needed to enable TurboKnots to handle very large diagrams. This led to the creation of an interface capable of taking in large diagrams in 4-tuple encoding, which I developed. Professor Wolf is continuing work on converting these diagrams into a net-encoding, which is crucial for simplifying these extremely large knots. Although progress has been made, ongoing work remains to complete the simplification routines and return a 4-tuple decomposition of the simplified links.
System Design and Architecture
The design and architecture of the TurboKnots web interface build on the foundation laid by previous students, who developed much of the general front-end design, formatting, and layout. This project focused on updating and enhancing the existing structure while integrating new functionality to accommodate the powerful capabilities of the TurboKnots program. The core technologies utilised were PHP and JavaScript, chosen for their flexibility in handling complex user interactions and back-end processes.
Frontend Design
The frontend, originally created by the previous developers, features a clean and intuitive layout, allowing users to easily navigate the various functionalities of TurboKnots. JavaScript powers the dynamic interactions within the user interface, such as real-time updates when manipulating knots or selecting different options for knot operations. The existing design elements were preserved and enhanced to ensure a seamless user experience across multiple devices and platforms.
 |
|---|
| The frontend design |
Backend Integration
The TurboKnots program is composed of several separate “modules”, developed by Professor Thomas Wolf, each designed to handle specific tasks. These modules receive input, perform complex calculations (such as knot simplification), and return the result. To integrate these modules with the web interface, PHP scripts were employed to facilitate communication between the user interface and the TurboKnots backend. When a user would input a request through the web interface, such as simplifying a knot or converting a knot in DT notation to Professor Thomas Wolf’s MiniKnot encoding, the input is sent to the appropriate TurboKnots module via PHP. After processing the input, the module returns the result, which is then returned to the JavaScript frontend to handle displaying the new knot.
Development Process
The development process for the TurboKnots web interface began with understanding the existing codebase, the TurboKnots Linux program, and the modules created by Professor Thomas Wolf. Early in the project, a large part of the time was devoted to learning about knot theory through The Knot Book [1] by Colin C. Adams. This knowledge was essential for the duration of the project. During the development of the TurboKnots web interface, I encountered a range of technical challenges that required investigation and problem-solving. Initially, I tested the interface made by the prior students and noted down everything that was not functioning properly. I made incremental improvements, such as moving the navigation bar and page footer to a separate PHP file for better organisation.
A critical problem emerged involving the truncation of outputs from the modules when called through a script. I initially thought it could have been an issue with PHP’s output buffer, but when the problem persisted with small Python and Shell scripts, I realised I was wrong. The problem continued when redirecting the output to a file, which led me to believe there was an issue with how the modules handled their output. After Professor Thomas Wolf made some changes to how the output of a module was served, I was able to successfully get the output.
Through these challenges, I improved the systems functionality, resolving issues that had caused the modules to fail to load or execute correctly. For example, once the script-handling issues were addressed, I discovered that the drawing of knots on the screen was not functioning as expected. I hypothesised that this was due to changes in how the mk (minimise knot) module returned the minimised knot. There had been improvements made to TurboKnots and its modules since the last student developers had worked on the project. Along with returning the minimised knot’s MiniKnot encoding, the module now also returns the names and number of each knot that the input decomposes into. Fixing this allowed the minimise knot button to work properly.
The entire process was an interactive cycle of debugging, testing, and implementing solutions, with each solution often leading to another challenge. However, by the end of this development cycle, I was able to implement a working system that integrates the complex TurboKnots calculations into a usable and functional web interface.
Achievements and Key Features
- Restored and improved critical portions of the TurboKnots web interface
- Restored functionality that had become outdated due to backend changes
- Enabled proper communication between TurboKnots modules and web interface
- Worked with modules developed by Professor Thomas Wolf
- Resolved permissions errors in a Linux environment
 |  |
|---|---|
| Before compressing the knot | After compressing the knot |
- Fixed core functionality including:
- Random knot generation
- Knot simplification
- Colouring knot
 | 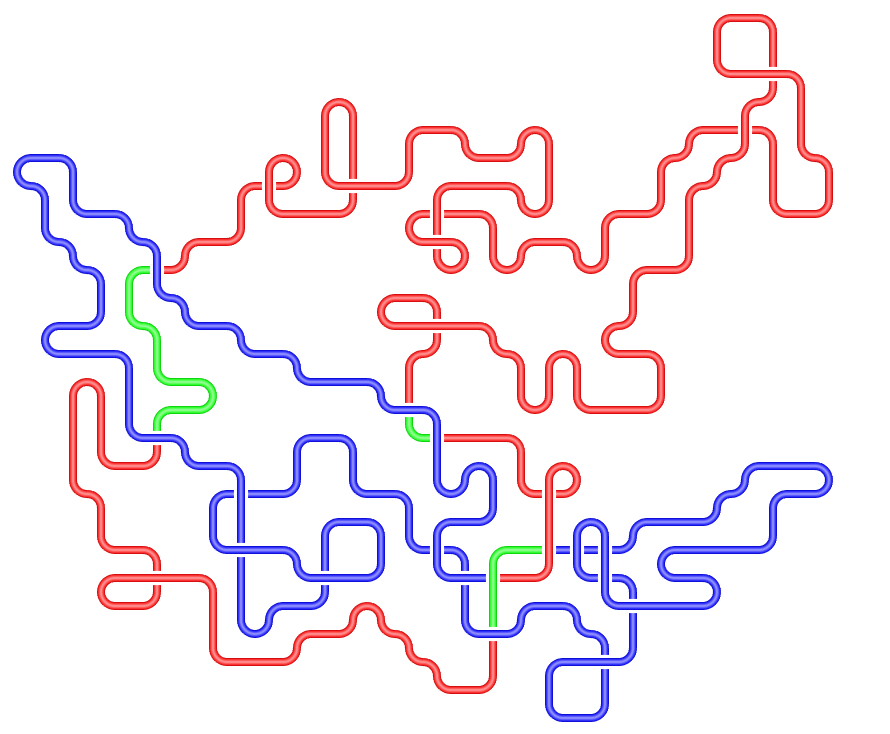 |  |
|---|---|---|
| A randomly generated knot | The same knot coloured | The same knot simplified |
- Implemented knot loading and visualisation by name
- Integrated complex data from the TurboKnots backend to the frontend
- Ensured accurate display of knots of varying complexities
 | 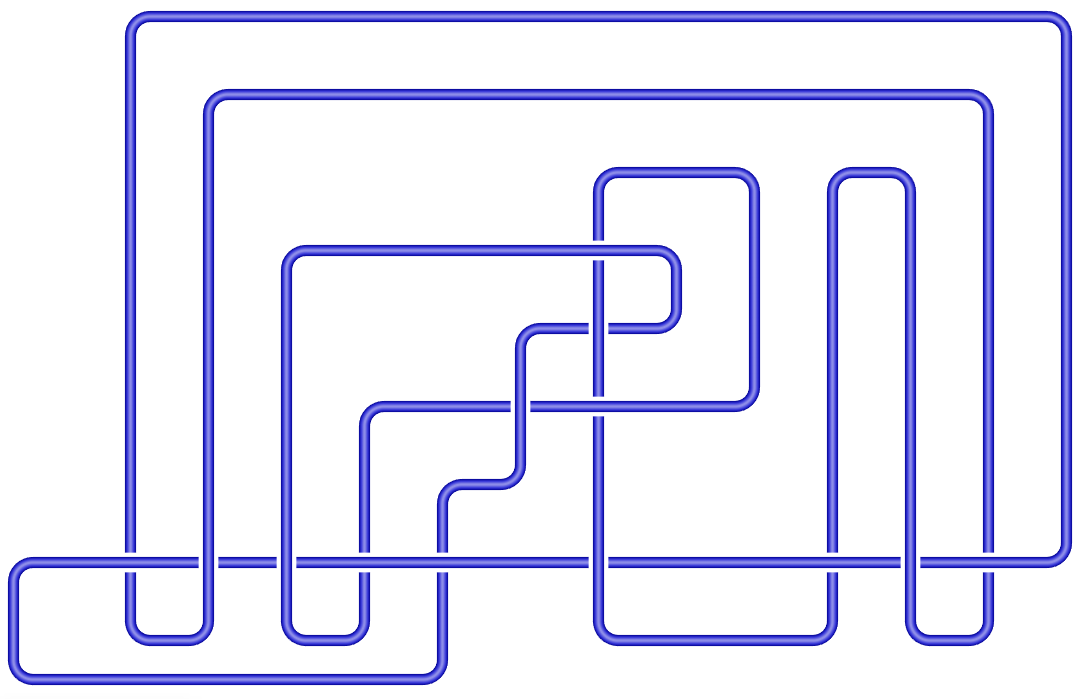 |
|---|---|
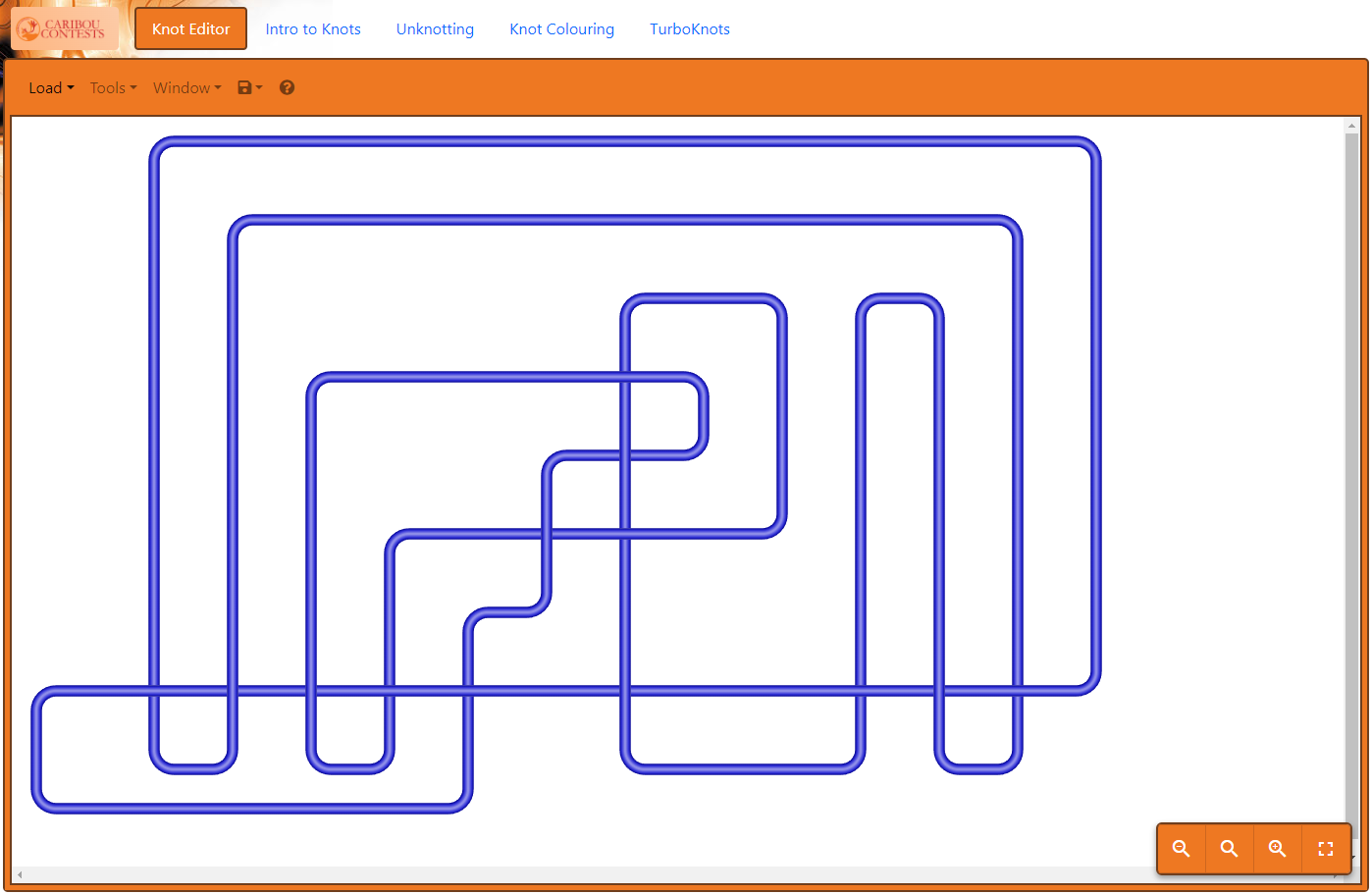
| Loading knot 13n15 by name | The knot loaded |
- Added feature for users to input knots from 4-tuple encoding and DT notation
 |  |
|---|---|
| Loading knot 13n15 by DT notation | The knot loaded |
- Developed and tested debugging strategies for future developers
Future Work and Improvements
Despite the progress made on the TurboKnots web interface, several changes and improvements can still be made. One potential addition is extending the knot analysis features by integrating more advanced invariants like the HOMFLY polynomial. Additionally, adding support for even more import/export formats and encodings would allow for the program to be even more accessible than it currently is.
An essential enhancement for the TurboKnots web interface would be to implement a hard disk based storage solution for the database. Currently, a substantial portion of the time required for knot simplification is spent loading the database into memory. This is a critical issue because the TurboKnots Linux program itself loads the database once at startup, which is relatively efficient. However, most modules within TurboKnots also need to access this database every time they are run. This repetitive loading of the database for each module causes substantial delays, leading to inefficient processing and longer wait times for users. By transitioning to a relational database system that supports on-disk storage, this memory-intensive loading process could be mitigated, thereby significantly reducing the overall processing time.
Conclusions
The development and enhancement of the TurboKnots web interface have significantly advanced the tool’s usability and functionality. By integrating a user-friendly interface with advanced features such as real-time knot simplification and support for multiple different knot encodings, the project has addressed many of the limitations present in existing knot theory based programs. This system’s ability to handle complex knots dynamically and display detailed information makes it a valuable resource for researchers and educators in the field of knot theory. The development process, though challenging, has been marked by substantial achievements, including overcoming technical hurdles and implementing key features. Moving forward, addressing performance issues, particularly by optimising database handling, will be crucial for further improving the efficiency and scalability of TurboKnots. Overall, the project represents a significant step forward in knot theory analysis, offering both in depth and flexibility in exploring and manipulating knots.
Bibliography
[1] Adams, C. C. (2010). The knot book: An elementary introduction to the mathematical theory of Knots. American Mathematical Society.
[2] Brock University. (n.d.). Thomas Wolf’s Publications. http://lie.math.brocku.ca/twolf/home/publications.html#4
[3] Caribou Contests. (n.d.). Knot Editor. https://cariboutests.com/games/knots/knoteditor/
[4] Cha, J. C., & Wong, M. (n.d.). KnotFinder. https://knotinfo.math.indiana.edu/homelinks/knotfinder.php
[5] Horowitz, J. (n.d.). Knot Identification Tool. https://joshuahhh.com/projects/kit/
[6] Miller, K. (n.d.). KnotFolio. https://knotfol.io/
[7] The Rolfsen Knot Table. Knot Atlas. (n.d.). https://katlas.org/wiki/The\_Rolfsen\_Knot\_Table