Connor's Notes

⬅️ Back to portfolio

COSC 3P95: Week 1 Notes

6 min read

Note

These notes are taken after the fact based on the slides. Anything mentioned only in lecture is not included. Starting from 1-Introduction to Analysis, slide 1.

Why Take This Course?

  • learn methods to improve software quality
    • reliability, security, performance
  • become a better software developer/tester
  • build specialized tools for software diagnosis & testing
  • for the war stories (real-world failures)

Case Study: Ariane Rocket Disaster (1996)

  • caused by a numeric overflow error
    • 64-bit sideways velocity stored in 16-bit space
    • overflow misinterpreted as signal to change course
  • cost:
    • hundreds of millions of dollars
    • multi-year setback to Ariane program
  • video link
  • post mortem

Security Vulnerabilities

  • exploits of errors in programs
  • examples:
    • Moonlight Maze (1998)
    • Code Red (2001)
    • Titan Rain (2003)
    • Stuxnet (2010)
  • modern issues:
    • malware on Android (2011 report: 0.5–1M users affected)
    • 3/10 Android users face web-based threat yearly
    • attackers = increasingly sophisticated

What is Program Analysis?

  • program analysis = body of work to discover useful facts about programs
flowchart LR
    A[Program Analyzer A] --> B[Program P]
    B -->|works correctly| C[OK]
    B -->|fails for some inputs| D[Bug]

Examples of Program Issues

// Dead Code Example
public class DeadCode {
  public static void main(String[] args) {
    System.out.println("Hello World");
    return;
    System.out.println("This is dead code"); // never runs
  }
}
 
// Intentional Memory Leak
public class MemoryLeak {
  public static void main(String[] args) {
    while (true) {
      Integer[] arr = new Integer[1000]; // no release
    }
  }
}

Facts About Programs (1)

  • Memory leaks → allocated but never freed
  • Dead code → never executed
  • Concurrency issues → race conditions / deadlocks
  • Input validation → e.g., prevent SQL injection, XSS
  • Code complexity → cyclomatic complexity (maintainability)

Facts About Programs (2)

  • API misuse → wrong usage = subtle bugs
  • Resource utilization → inefficient CPU/disk
  • Type errors → mismatches (esp. in weakly typed languages)
  • Uninitialized variables → undefined behaviour
  • Exception handling → paths where exceptions may go unhandled

Other Interesting Questions

  • does the program terminate on all inputs?
  • how large can the heap become?
  • can sensitive info leak to untrusted users?
  • can untrusted users affect sensitive info?
  • are buffer overruns possible?
  • data races? SQL injection? XSS?

Program Points & Invariants

  • program point: any value of program counter (any line of code)
  • invariant: property that holds at a program point across all inputs/executions
foo(p, x) {
  var f, q;
  if (*p == 0) { f = 1; }
  else {
    q = alloc 10;
    *q = (*p) - 1;
    f = (*p) * (x(q, x));
  }
  return f;
}

Questions:

  • will x be read later?
  • can pointer p be null?
  • which vars can p point to?
  • is x initialized before read?
  • lower/upper bounds on x?
  • do p and q point to disjoint heap structures?
  • can an assert fail here?

Why These Answers Matter

  • efficiency: optimize resources
  • correctness: verify behaviour & catch bugs
  • program understanding
  • enable refactoring

Types of Program Analysis

  • Static analysis → compile-time, inspects code
  • Dynamic analysis → run-time, monitors execution
  • Hybrid → combines both

Static Analysis

  • infers facts from code without execution
  • tools/examples:
    • Lint, FindBugs, Coverity (error patterns)
    • Microsoft SLAM (API usage rules)
    • Facebook Infer (memory leaks)
    • ESC/Java (verify invariants)

Quiz: Program Invariants

int p(int x) { return x * x; }
 
void main() {
  int z;
  if (getc() == 'a')
    z = p(6) + 6;
  else
    z = p(-7) - 7;
}

At the end of the program, the value of z is always the same no matter which branch executes.  

Discovering Invariants (Static Analysis)

  • some invariants are definitely true (e.g., z == 42)
  • some are maybe invariants
  • some are definitely not invariants

Dynamic Program Analysis

  • infers facts by monitoring actual executions
  • tools/examples:
    • Purify (array bound checking)
    • Eraser (data race detection)
    • Valgrind (memory leaks)
    • Daikon (likely invariants)

Anatomy of a Static Analysis

Key components:

  • Intermediate Program Representation → CFGs, ASTs, bytecode
  • Abstract domain → approximate states
  • Transfer functions → update state per statement
  • Fixed-point algorithm → iterative approximation until states stop changing

Terminology

  • control-flow graph (CFG)
  • abstract vs concrete states
  • termination
  • completeness
  • soundness

Control Flow Graphs (CFGs)

  • directed graph of program flow
    • nodes = statements
    • edges = control flow
  • has one entry + one exit
  • predecessor nodes = pred(v), successor nodes = succ(v)
flowchart TD
    A[start] --> B[f=1]
    B -->|n>0| C[f=f*n]
    C --> D[n=n-1]
    D --> B
    B -->|false| E[return f]

CFG Construction

A Control Flow Graph (CFG) models all possible paths of execution in a program. You build it inductively from the code:

  • Simple statements (assignment, declaration, return, output) → one node each.
  • Sequence S1; S2; → connect the exit of S1 to the entry of S2.
  • Conditional (if ... else ...) → one decision node with two outgoing edges: true and false; both rejoin after their subgraphs.
  • Loops (while, for) → a decision node whose true edge enters the body and whose false edge exits the loop; the body flows back to the decision node, forming a cycle.
  • Entry/Exit → every CFG has a single entry and a single exit (they can be no-ops).

Simple Statements

flowchart LR
    A[entry] --> S[x = y + 1]
    S --> E[exit]

flowchart LR
    A[entry] --> S1[x = 0]
    S1 --> S2[y = x + 7]
    S2 --> E[exit]

flowchart TD
    A[entry] --> C{c}
    C -->|true| S1[x = x + 1]
    C -->|false| S2[x = x - 1]
    S1 --> J[join]
    S2 --> J
    J --> E[exit]

flowchart TD
    A[entry] --> C{c}
    C -->|true| B[body S]
    B --> C
    C -->|false| E[exit]

Normalization

  • break complex expressions into single steps
  • use fresh variables
x = f(y+3)*5;
// normalized
t1 = y+3;
t2 = f(t1);
x = t2*5;

Example Static Analysis Problem

  • goal: find vars with constant values at program points
  • method:
    1. draw CFG
    2. apply iterative approximation

Iterative Approximation

  • method: start with guess → refine repeatedly until fixed point
  • used for constant propagation, etc.
flowchart TD
    A[z=3] --> B{while true}
    B -->|x==1| C[y=7]
    B -->|else| D[y=z+4]
    C --> E[assert y==7]
    D --> E
    E --> B

Iterative Approximation Quiz

b = 1;
while (true) {
  b = b + 1;
}
  • what does analysis infer for b at:
    1. loop header
    2. entry of loop body
    3. exit of loop body

Overview of Static Analysis

  • representation: CFG, AST, bytecode
  • abstract domain: approximate states
  • transfer function: how statements affect abstract state
  • fixed-point algorithm: converge to stable state

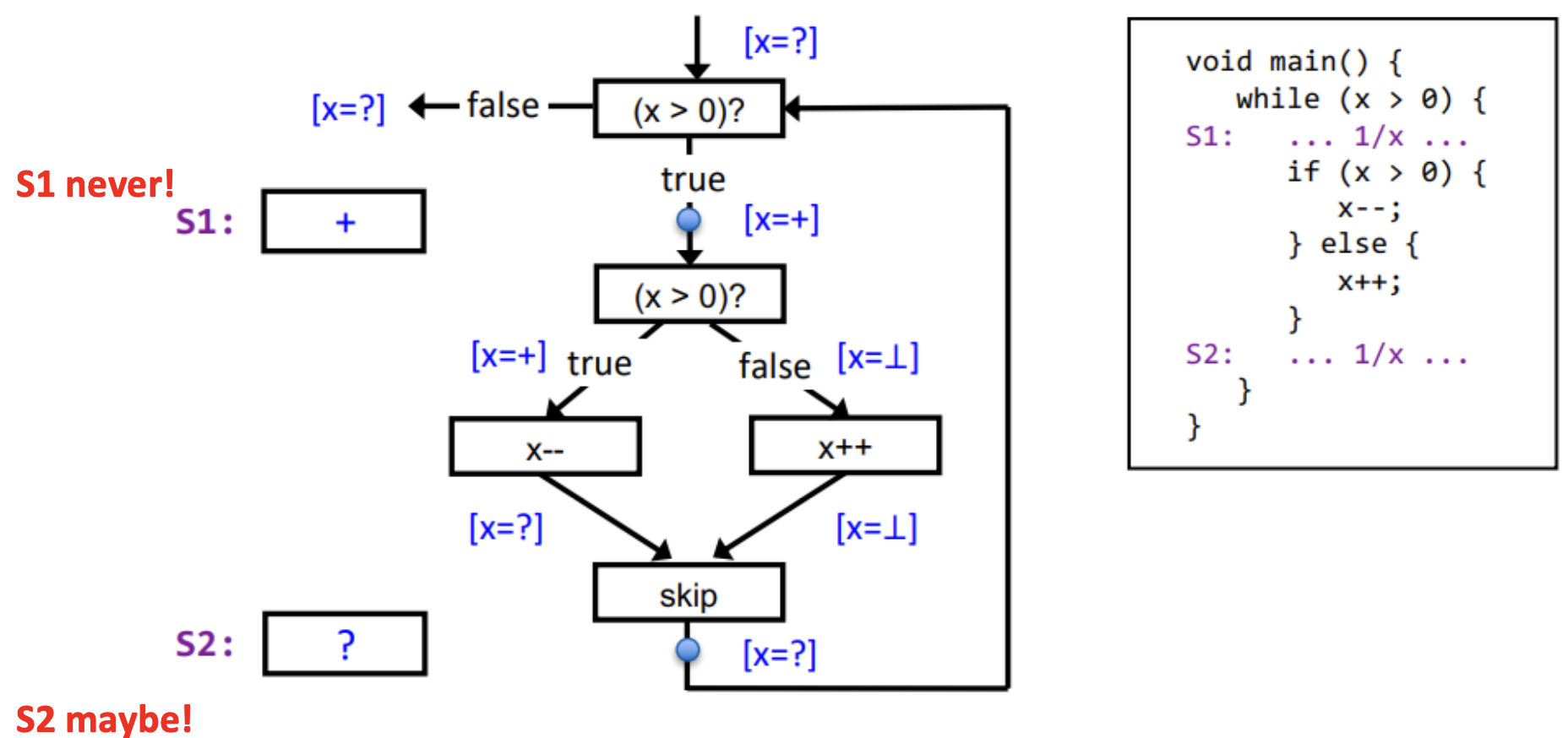
Quiz: Divide-by-Zero Example

  1. draw CFG
  2. analyze with iterative approximation
  3. classify statements:
    • never divides by zero
    • may divide by zero

Trade-offs in Software Analysis

  • Static analysis
    • proportional to program size
    • sound (no false positives) but often incomplete
  • Dynamic analysis
    • proportional to execution time
    • complete for observed runs but not sound (may miss bugs)

Graph View