Note
Started slide 1 of
l7Oa.pdf(week 4)
Shared-memory programming with OpenMP
OpenMP
API for shared-memory programming
- designed for systems in which each thread or process can potentially have access to all available memory
- Team: collection of threads executing the parallel block → original thread and new threads
- Master: the original thread
- Slave/worker: additional threads created
Pragmas
API for shared-memory programming
- C/C++
- compilers that do not support the pragmas ignore them
// omp_hello.c
#include <stdio.h>
#include <stdlib.h>
#include <omp.h>
void Hello(void); /* Thread function */
int main(int argc, char* argv[]) {
/* Get number of threads from command line */
int thread_count = strtol(argv[1], NULL, 10);
#pragma omp parallel num_threads(thread_count)
Hello();
return 0;
} /* main */
void Hello(void) {
int my_rank = omp_get_thread_num();
int thread_count = omp_get_num_threads();
printf("Hello from thread %d of %d\n", my_rank, thread_count);
} /* Hello */compiling and running:
gcc -g -Wall -fopenmp -o omp_hello omp_hello.c
./omp_helloClause
- text that modifies a directive
- the
num_threadsclause can be added to a parallel directive - allows programmer ot specify the number of threads that should execute the following block
# pragma omp parallel num_threads(thread_count)The trapezoidal rule
Serial algorithm
/* Input: a, b, n */
h = (b - a) / n;
approx = (f(a) + f(b)) / 2.0;
for (i = 1; i <= n - 1; i++) {
x_i = a + i * h;
approx += f(x_i);
}
approx = h * approx;A first OpenMP version
- we identified two types of task
- computation of the areas of individual trapezoids
- adding the areas of the trapezoids
- there is no communication between the tasks in the first collection
- each task is completely independent, but each task communicates with 1.2
- we assumed that there would be many more trapezoids than cores
- we aggregate tasks by assigning a contiguous block of trapezoids to each thread → single thread to each core
Assigning trapezoids to threads
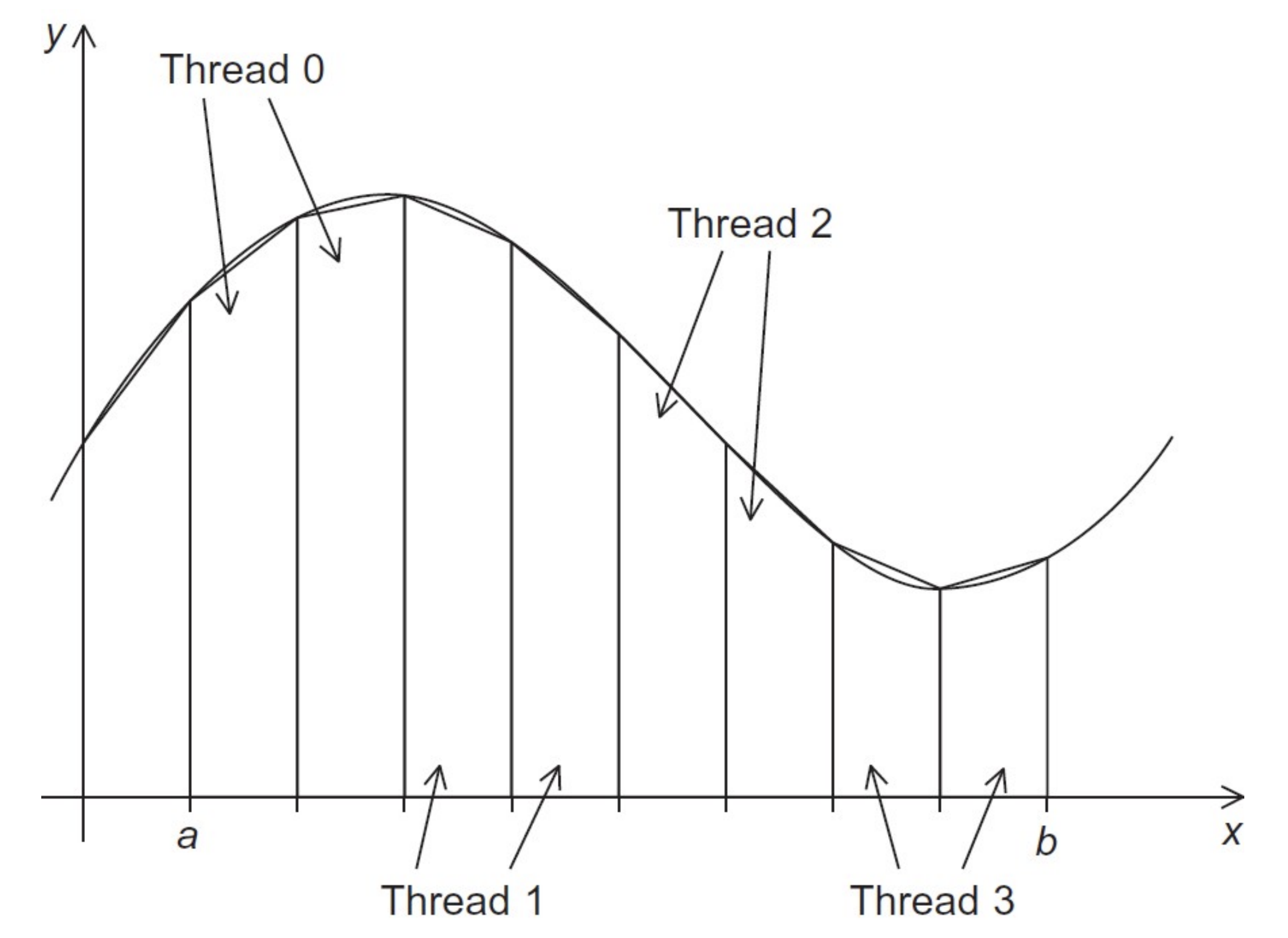
| Time | Thread 0 | Thread 1 |
|---|---|---|
| 0 | global_result = 0 to register | finish my_result |
| 1 | my_result = 1 to register | global_result = 0 to register |
| 2 | add my_result to global_result | my_result = 2 to register |
| 3 | store global_result = 1 | add my_result to global_result |
| 4 | store global_result = 2 |
// BAD:
global_result += my_result; // causes race condition
// GOOD:
# pragma omp critical // prevents race condition
global_result += my_result;Mutual exclusion
#include <stdio.h>
#include <stdlib.h>
#include <omp.h>
void Trap(double a, double b, int n, double* global_result_p);
int main(int argc, char* argv[]) {
double global_result = 0.0; /* Store result in global_result */
double a, b; /* Left and right endpoints */
int n; /* Total number of trapezoids */
int thread_count;
thread_count = strtol(argv[1], NULL, 10);
printf("Enter a, b, and n\n");
scanf("%lf %lf %d", &a, &b, &n);
# pragma omp parallel num_threads(thread_count)
Trap(a, b, n, &global_result);
printf("With n = %d trapezoids, our estimate\n", n);
printf("of the integral from %f to %f = %.14e\n",
a, b, global_result);
return 0;
} /* main */
void Trap(double a, double b, int n, double* global_result_p) {
double h, x, my_result;
double local_a, local_b;
int i, local_n;
int my_rank = omp_get_thread_num();
int thread_count = omp_get_num_threads();
h = (b-a)/n;
local_n = n/thread_count;
local_a = a + my_rank*local_n*h;
local_b = local_a + local_n*h;
my_result = (f(local_a) + f(local_b))/2.0;
for (i = 1; i <= local_n-1; i++) {
x = local_a + i*h;
my_result += f(x);
}
my_result = my_result*h;
# pragma omp critical
*global_result_p += my_result;
} /* Trap */Scope in OpenMP
- Shared scope: a variable that can be accessed by all the threads in the team
- default for variables declared before a parallel block
- Private scope: a variable that can only be accessed by a single thread
Reduction clause
- we need this more complex version to add each thread’s local calculation to get
global_result
void Trap(double a, double b, int n, double* global_result_p);- though, we would prefer this
double Trap(double a, double b, int n);
global_result = Trap(a, b, n);- if we use this, there is no critical section
double Local_trap(double a, double b, int n);- if we fix it like this, we force the threads to execute sequentially:
global_result = 0.0;
#pragma omp parallel num_threads(thread_count)
{
#pragma omp critical
global_result += Local_trap(double a, double b, int n);
}- we can avoid this problem by declaring a private variable inside the parallel block & moving the critical section after the function call
global_result = 0.0;
#pragma omp parallel num_threads(thread_count)
{
double my_result = 0.0; /* private */
my_result += Local_trap(double a, double b, int n);
#pragma omp critical
global_result += my_result;
}Reduction operators
- Reduction operator: a binary operation such as addition or multiplication
- Reduction: a computation that repeatedly applies the same reduction operator to a sequence of operands to get a single result
- all of the intermediate results of the operation should be stored in the same variable
- a reduction clause can be added to a parallel directive
#reduction(<operator>:<variable list>)
// where <operator> = one of [+, *, -, &, |, ^, &&, ||]global_result = 0.0;
#pragma omp parallel num_threads(thread_count) \ reduction(+: global_result)
{
global_result += Local_trap(double a, double b, int n);
}Parallel for directive
forks a team of threads to execute the following structured block
- but, the structured block following the parallel for directive must be a for loop
- with parallel for directive, the system parallelizes the for loop by dividing the iterations of the loop among threads
// bad
h = (b - a) / n;
approx = (f(a) + f(b)) / 2.0;
for (i = 1; i <= n - 1; i++)
approx += f(a + i * h);
approx = h * approx;
// good
h = (b - a) / n;
approx = (f(a) + f(b)) / 2.0;
#pragma omp parallel for num_threads(thread_count) \ reduction(+: approx)
for (i = 1; i <= n - 1; i++)
approx += f(a + i * h);
approx = h * approx;Acceptable for statements

Data dependencies
since the result is dependent on data from the last loop iteration, it is not good for parallel
// bad
fibo[0] = fibo[1] = 1;
for (i = 2; i < n; i++)
fibo[i] = fibo[i - 1] + fibo[i - 2];
// also bad
fibo[0] = fibo[1] = 1;
#pragma omp parallel for num_threads(2)
for (i = 2; i < n; i++)
fibo[i] = fibo[i - 1] + fibo[i - 2];What happened?
- OpenMP compilers do not check for dependences among iterations in a loop, when the loop is parallelized with a parallel for directive
- a loop in which the results of one or more iterations depends on other iterations cannot be correctly parallelized by OpenMP
Estimating
Non-parallel code:
double factor = 1.0;
double sum = 0.0;
for (k = 0; k < n; k++) {
sum += factor / (2 * k + 1);
factor = -factor;
}
pi_approx = 4.0 * sum;OpenMP solution #1
double factor = 1.0;
double sum = 0.0;
#pragma omp parallel for num_threads(thread_count) reduction(+:sum)
for (k = 0; k < n; k++) {
sum += factor / (2 * k + 1);
factor = -factor; // loop dependency issue here
}
pi_approx = 4.0 * sum;OpenMP solution #2
double sum = 0.0;
#pragma omp parallel for num_threads(thread_count) \ reduction(+:sum) private(factor)
// ensures factor has private scope
for (k = 0; k < n; k++) {
if (k % 2 == 0)
factor = 1.0;
else
factor = -1.0;
sum += factor / (2 * k + 1);
}
pi_approx = 4.0 * sum;Note
Ended slide 49