COSC 3P93: Lecture 11

Performance

Why aren’t parallel applications scalable?

• sequential performance
• critical paths (dependencies between computations spread across processors)
• bottlenecks (one processor holds things up)
• algorithmic overhead (some things just take more effort to do in parallel)
• communication overhead (spending increasing proportion of time on communication)
• load imbalance (makes all processors wait for the slowest one, dynamic behaviour)
• speculative loss (do A and B in parallel, but B is ultimately not needed → wasted work from speculative execution)

What is the maximum parallelism possible?

• depends on application, algorithm, program → data dependencies in execution
• MaxPar:
  • analyzes the earliest possible “time” any data can be computed
  • assumes a simple model for time it takes to execute instruction or go to memory
  • result is the maximum parallelism available

Embarrassingly parallel computations

• no or very little communication between processes
• each process can do its tasks without any interaction with other processes

Calculating $\pi$ with Monte Carlo

• place a circle inside a square box with side of $2\ast \text{radius}$ (2cm)
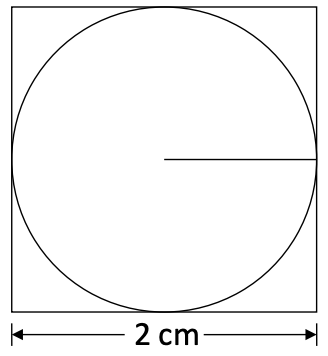
• the ratio of the circle area to the square area is

$$\frac{\text{area of circle}}{\text{area of square}}=\frac{\pi r^2}{(2r{)}^2}=\frac{\pi }{4}$$

• randomly choose a number of points in the square → for each point $p$, determine if $p$ is inside the circle
• the ratio of points in the circle to points in the square will give approximation of $\frac{\pi }{4}$

Analytical / theoretical techniques

• involves simple algebraic formulas and ratios
  • typical variables: data size ($N$), number of processors ($P$), machine constants
  • to model performance of individual operations, components, algorithms in terms of the above
    • be careful to characterize variations across processors
    • model them with max operators
  • constants are important in practice
    • use asymptotic analysis carefully

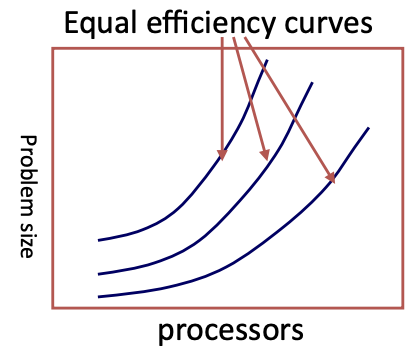
Isoefficiency

• goal is to quantify scalability
• how much increase in problem size is needed to retain the same efficiency on a larger machine?
• efficiency:
  • $T_1/(p\ast T_P)$
  • $T_P=\text{computation}+\text{communication}+\text{idle}$
• isoefficiency:
  • equation for equal-efficiency curves
  • if no solution → problem is not scalable in the sense defined by isoefficiency
  • how the problem size ($S$) must increase with the number of processors ($P$) to keep the efficiency ($E$) constant

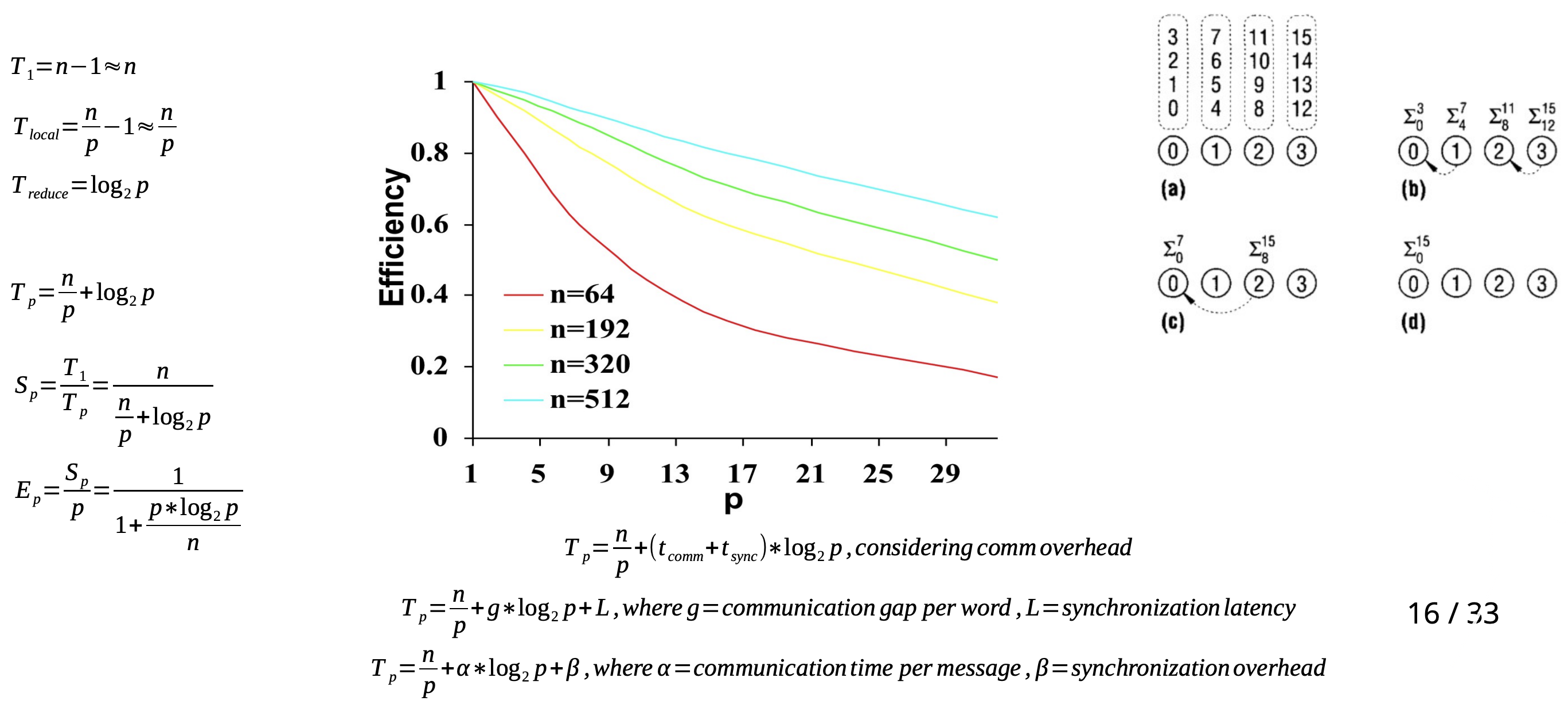
Scalability of adding $n$ numbers

• scalability of a parallel system is a measure of its capacity to increase speedup with more processors
• adding $n$ numbers ($n$ sums) on $p$ processors with strip partition

Problem size and overhead

• informally, problem size is expressed as a parameter of the input size
• a consistent definition of the size of the problem is the total number of basic operations ($T_{seq}$) → also refere to problem size as work ($W=T_{seq}$)
• overhead of a parallel system ($T_O$) is defined as the part of the cost not in the best serial algorithm
• denoted by $T_O$, it is a function of $W$ and $p$
  • $T_O(W,p)=p{T}_{par}-W$ ($p{T}_{par}$ includes overhead)
  • $T_O(W,p)+W=p{T}_{par}$

Isoefficiency function

• with fixed efficiency, $W$ as a function of $p$

Isoefficiency function of adding $n$ numbers

• overhead function: $T_O(W,p)=p{T}_{par}-W=2plog(p)$
• isoefficiency function: $W=K\ast 2plog(p)$
• if $p$ doubles, $W$ needs to also be doubled to roughly maintain the same efficiency
• isoefficiency functions can be more difficult to express for more complex algorithms

More complex isoefficiency functions

• a typical overhead function $T_O$ can have several distinct terms of different orders of magnitude with respect to both $p$ and $W$
• we can balance $W$ against each term of $T_O$ and compute the respective isoefficiency functions for individual terms
  • keep only the term that requires the highest grow rate with respect to $p$

→ my notes end at slide 20

take notes on rest of slides

l4b.pdf

finished